Question

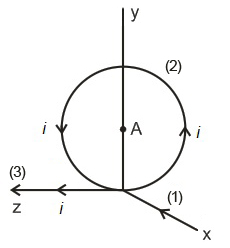
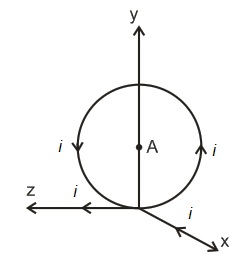
A ring of the radius $R$ is placed in the $y-z$ plane and it carries a current $i$ . The conducting wires which are used to supply the current to the ring can be assumed to be very long and are placed as shown in the figure. The magnitude of the magnetic field at the centre of the ring $A$ is

• A. $\frac{\left(\mu \right)_{0} \textit{i}}{4 \pi \textit{R}}\sqrt{2 \left(2 \left(\pi \right)^{2} - 2 \pi + 1\right)}$
• B. $\frac{\left(\mu \right)_{0} i}{4 \pi R}\sqrt{3 \left(2 \left(\pi \right)^{2} - 2 \pi + 1\right)}$
• C. $\frac{\left(\mu \right)_{0} i}{3 \pi R}\sqrt{3 \left(2 \left(\pi \right)^{2} + 2 \pi - 1\right)}$
• D. $\frac{\left(\mu \right)_{0} i}{3 \pi R}\sqrt{3 \left(2 \left(\pi \right)^{2} + 2 \pi + 1\right)}$

Answer 1

Answer: (A)

​
Magnetic field due to wire along $x$ - axis at $A$
$\overrightarrow{ B }_{1}=\frac{\mu_{0}}{4 \pi} \frac{i}{ R }(-\hat{ k })$
Magnetic field due to loop in $y z$ - plane at $A$
$\overrightarrow{ B }_{2}=\frac{\mu_{0}}{4 \pi} \frac{2 \pi i}{ R }(\hat{ i })$
Magnetic field due to wire along $z$ -axis at $A$
$\overrightarrow{ B }_{3}=\frac{\mu_{0}}{4 \pi} \frac{i}{ R }(-\hat{ i })$
$\overrightarrow{ B }=\overrightarrow{ B }_{1}+\overrightarrow{ B }_{2}+\overrightarrow{ B }_{3}$
$\begin{aligned} &=\frac{\mu_{0}}{4 \pi} \frac{i}{ R }(2 \pi-1) \hat{ i }+\frac{\mu_{0}}{4 \pi} \frac{i}{ R }(\widehat{ k }) \\ B &=\frac{\mu_{0}}{4 \pi} \frac{i}{ R } \sqrt{(2 \pi-1)^{2}+1} \\ &=\frac{\mu_{0}}{4 \pi} \quad \frac{i}{ R } \sqrt{2\left(2 \pi^{2}-2 \pi+1\right)} \end{aligned}$