Q.
A ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass $\frac{M}{8}$ at rest at O. These masses can moveradially outwards along two massless rods fixed on the ring as shown in the figure. At some instant theangular speed of the system is $\frac{8}{9} ω$ and one of the masses is at a distance of $\frac{3}{5} R$ from O. At this instant the distance of the other mass from O is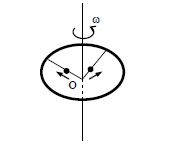
JEE AdvancedJEE Advanced 2015
Solution: