Question

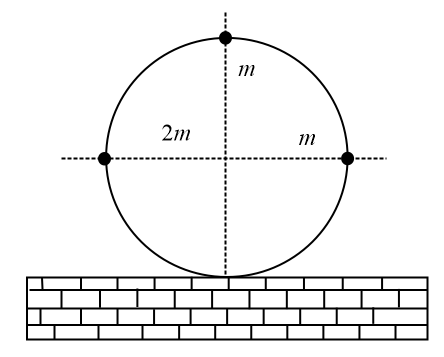
A ring of mass $m$ and radius $R$ has three particles attached to the ring as shown in the figure. The centre of the ring has a speed $v_{0}$ . The kinetic energy of the system is (slipping is absent),

• A. $6mv_{o}^{2}$
• B. $12mv_{0}^{2}$
• C. $4mv_{0}^{2}$
• D. $8mv_{0}^{2}$

Answer 1

Answer: (A)

As the ring is rolling without slipping,
$v_{0}=\omega r$ .
The velocity of particle at point $A$ can be given by,
$v_{A}=\sqrt{v_{0}^{2} + v_{0}^{2}}=\sqrt{2}v_{0}$ .
The velocity of particle at point $B$ can be given by,
$v_{B}=2v_{0}$ .
The velocity of particle at point $C$ can be given by,
$v_{C}=\sqrt{v_{0}^{2} + v_{0}^{2}}=\sqrt{2}v_{0}$ .
Now, the total kinetic energy of the system can be calculated by summing up kinetic energy of the particles and the total kinetic energy of the ring.
$KE=\frac{1}{2}m\left(v_{0}\right)^{2}+\frac{1}{2}I\left(\omega \right)^{2}+\frac{1}{2}\left(2 m\right)\left(v_{A}\right)^{2}+\frac{1}{2}\left(m\right)\left(v_{B}\right)^{2}+\frac{1}{2}\left(m\right)\left(v_{C}\right)^{2}$
$KE=\frac{1}{2}m\left(v_{0}\right)^{2}+\frac{1}{2}\left(m r^{2}\right)\left(\frac{\left(v_{0}\right)^{2}}{r^{2}}\right)+\frac{1}{2}\left(2 m\right)\left(2 \left(v_{0}\right)^{2}\right)+\frac{1}{2}\left(m\right)\left(4 \left(v_{0}\right)^{2}\right)+\frac{1}{2}\left(m\right)\left(2 \left(v_{0}\right)^{2}\right)$
$KE=6mv_{0}^{2}$ .