Question

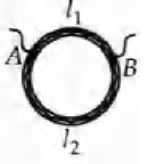
A ring is made of a wire having a resistance $R_0=12\, \Omega$. Find the points $A$ and $B$, as shown in the figure, at which a current carrying conductor should be connected so that the resistance $R$ of the sub circuit between these points is equal to $\frac{8}{3} \Omega$

• A. $\frac{l_1}{l_2}=\frac{5}{8}$
• B. $\frac{l_1}{l_2}=\frac{1}{3}$
• C. $\frac{l_1}{l_2}=\frac{3}{8}$
• D. $\frac{l_1}{l_2}=\frac{1}{2}$

Answer 1

Answer: (D)

Let $x$ be resistance per unit length of the wire.
Then,
The resistance of the upper portion i$R_{1}=x l_{1}$
The resistance of the lower portion is $R_{2}=x l_{2}$
Equivalent resistance between $A$ and $B$ is
$R=\frac{R_{1} R_{2}}{R_{1}+R_{2}}=\frac{\left(x l_{1}\right)\left(x l_{2}\right)}{x l_{1}+x l_{2}}$
$\frac{8}{3}=\frac{x l_{1} l_{2}}{l_{1}+l_{2}}$
or $\frac{8}{3}=\frac{x l_{1} l_{2}}{l_{2}\left(\frac{l_{1}}{l_{2}}+1\right)}$
or $\frac{8}{3}=\frac{x l_{1}}{\left(\frac{l_{1}}{l_{2}}+1\right)} \ldots$ (i)
Also $ R_{0}=x l_{1}+x l_{2} $
$12=x\left(l_{1}+l_{2}\right) $
$12=x l_{2}\left(\frac{l_{1}}{l_{2}}+1\right) \ldots (ii) $
Divide (i) by (ii), we get
$\frac{\frac{8}{3}}{12}=\frac{\frac{x l_{1}}{\left(\frac{l_{1}}{l_{2}}+1\right)}}{x l_{2}\left(\frac{l_{1}}{l_{2}}+1\right)}$
or $\frac{8}{36}=\frac{l_{1}}{l_{2}\left(\frac{l_{1}}{l_{2}}+1\right)^{2}}$
$\left(\frac{l_{1}}{l_{2}}+1\right)^{2} \frac{8}{36}=\frac{l_{1}}{l_{2}}$
or $\left(\frac{l_{1}}{l_{2}}+1\right)^{2} \frac{2}{9}=\frac{l_{1}}{l_{2}}$
Let $y=\frac{l_{1}}{l_{2}}$
$\therefore 2(y+1)^{2}=9 y $
or $ 2 y^{2}+2+4 y=9 y $
or $ 2 y^{2}-5 y+2=0$
Solving this quadratic equation, we get
$y=\frac{1}{2} $ or $2$
$ \therefore \frac{l_{1}}{l_{2}}=\frac{1}{2}$