1. Tardigrade
  2. Question
  3. Physics
  4. A ring has charge Q and radius R. If a Charge q is placed at its Center then the increase in tension in the ring is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. A ring has charge Q and radius R. If a Charge q is placed at its Center then the increase in tension in the ring isPhysics Question Image

Electrostatic Potential and Capacitance

Solution:

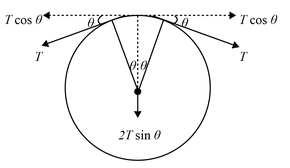
$T$ is tension in the ring.
Electrostatic force in radial direction will balance the tension component in that direction
$ 2 T \sin \theta=\frac{ qQ (2 \theta R )}{\frac{2 \pi R }{4 \pi \varepsilon_{0} R ^{2}}}
$
angle $\theta$ is very small then $\sin \theta=\theta$


$2 T \theta =\frac{ qQ 2 \theta}{8 \pi^{2} \varepsilon_{0} R ^{2}} $
$T = \frac{ qQ }{8 \pi^{2} \varepsilon_{0} R ^{2}}$

Solution Image