Q.
A rigid insulated wire frame in the form of a right angled
triangle ABC, is set in a vertical plane as shown in figure.
Two beads of equal masses m each and carrying charges $q_1$
and $q_2$ are connected by a cord of length l and can slide
without friction on the wires.
Considering the case when the beads are stationary
determine
(a) (i) The angle $\alpha$
(ii) The tension in the cord
(iii) The normal reaction on the beads
(b) If the cord is now cut what are the value of the charges for
which the beads continue to remain stationary?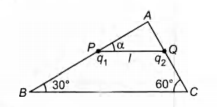
IIT JEEIIT JEE 1978Electrostatic Potential and Capacitance
Solution:
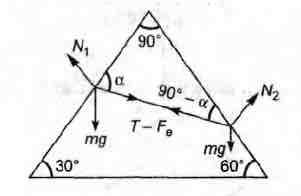
Tension and electrostatic force are in opposite direction and
along the string. Now each bead is in equilibrium under three
concurrent forces
(i) Normal reaction (N)
(ii) Weight (mg) and
(iii) $T-F_e,$ where $ F_e=\frac{1}{4\pi \varepsilon_0}.\frac{q_1q_2}{l^2}$
Applying Lami's theorem for both beads.
$ \frac{N_1}{sin\, (120- \alpha)}=\frac{mg}{cos\, \alpha}=\frac{T-F_e}{cos\, 60^\circ}$...(i)
$ \frac{N_2}{sin\, (60+ \alpha)}=\frac{mg}{sin\, \alpha}=\frac{T-F_e}{cos\, 30^\circ}$...(ii)
Dividing Eq. (i) by Eq. (ii), we have
$ tan\, \alpha=\frac{cos\, 30^\circ}{cos\, 60^\circ} = \sqrt 3 $
$\therefore \alpha = 60^\circ $
$ T=F_e+mg=\bigg(\frac{1}{4 \pi\varepsilon_0}\bigg).\frac{q_1q_2}{l^2}+mg\, \, \, \, $...(iii)
$ N_1 =\sqrt3\, mg$ and $N_2 = mg$
From Eq. (iii) T - 0 when string is cut.
or $ q_1q_2 = - (4 \pi\varepsilon_0) mgl^2$