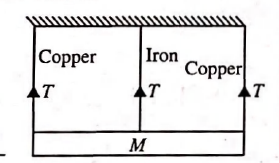
Question

A rigid bar of mass $M$ is supported symmetrically by three wires each of length $L$. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to

• A. $\frac{Y_{copper}}{Y_{iron}}$
• B. $\sqrt{\frac{Y_{iron}}{Y_{copper}}}$
• C. $\frac{Y_{iron}^{2}}{Y^{2}_{copper}}$
• D. $\frac{Y_{iron}}{Y_{copper}}$

Answer 1

Answer: (B)

The situation is as shown in the figure.
Let $T$ be tension in each wire.
As the bar is supported symmetrically by the three wires, therefore extension in each wire is same.
As $Y=\frac{F/ A}{\Delta L /L}$
If D is the diameter of the wire,

then $Y=\frac{F/ \pi\left(D /2\right)^{2}}{\Delta L/ L}$ $=\frac{4 FL}{\pi D^{2}\Delta L}$
As per the conditions of the problem, $F \left(tension\right)$, length $L$, and extension $\Delta L$ is same for each wire.
$\therefore $$\quad$ $Y\propto \frac{1}{D^{2}} $ $\quad$ or $D\propto\sqrt{\frac{1}{Y}}$ $\quad$ $\therefore $ $\quad$ $\frac{D_{copper}}{D_{iron}}$ $=\sqrt{\frac{Y_{iron}}{Y_{copper}}}$