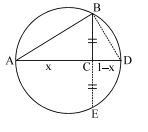
Q. A right triangle is drawn in a semicircle of radius $\frac{1}{2}$ with one of its legs along the diameter. The maximum area of the triangle is
Application of Derivatives
Solution:
$( BC )( CE )= x (1- x ) (\text { property of circle) }[ AC = x ; CD =1- x ]$
but $ BC = CE$
$\therefore BC =\sqrt{ x (1- x )} $
$A =\frac{ x \sqrt{ x - x ^2}}{2} \text {. Now maximise } A .$
$A _{\max }$ occurs at $x =\frac{3}{4}$