Q.
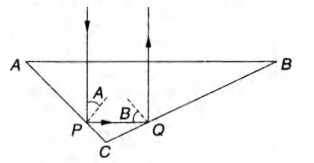
A right angled prism is to be made by selecting a proper material and the angles A and B $(B \le A),$ as shown in figure. It is desired that a ray of light incident on the face AB emerges parallel to the incident direction after two internal reflections.
(a) What should be the minimum refractive index n for this to be possible ?
(b) For n = 5/3 is it possible to achieve this with the angle B equal to 30 degrees ?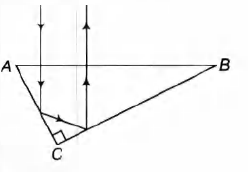
IIT JEEIIT JEE 1987
Solution:
(a) At P, angle of incidence $i_A$ = A
and at Q, angle of incidence $i_B$ = B
If T1R satisfies for the smaller angle of incidence than for
larger angle of incidence is automatically satisfied.
$B \le A \, \, \, \, \, \, \therefore \, \, \, \, \, \, \, \, i_B \le i_A$
Maximum value of B can be $45^\circ$. Therefore, if condition of
TIR is satisfied, then condition of TIR will be satisfied for all
value of $i_A and i_B$
Thus, $\, \, \, \, \, \, \, \, \, \, \, 45^\circ \ge \theta_c$
$or sin 45^\circ \ge sin \theta_c$
$or \frac{1}{\sqrt{2}} \ge \frac{1}{\mu} or \mu \ge \sqrt{2}$
$\therefore $ $\mu or\, n\, is \sqrt{2}.$
$(b) For\, n=\frac{5}{3}, sin \theta_c=\frac{1}{n}=sin^{-1}\Bigg(\frac{3}{5}\Bigg)\approx 37^\circ$
$If \, \, \, \, \, \, =30^\circ, then \, \, \, \, i_B=30^\circ$
$then \, \, \, \, \, \, =60^\circ\, or\, \, \, \, \, i_A=60^\circ$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, i_A > \theta_c but i_B < \theta_c$
i.e. TIR will take place at A but not at B.
or we write : sin $i_B < sin \theta_c < sin\, i_A$
$or sin 30^\circ < \frac{3}{5} < sin 60^\circ$
$or 0.5 < 0.6 < 0.86$