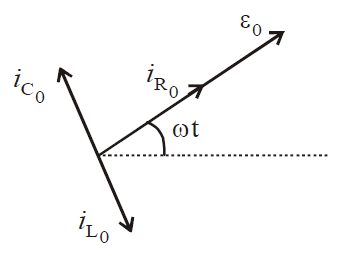
Q. A resistor of resistance $R$, capacitor of capacitance $C$ and inductor of inductance $L$ are connected in parallel to $A C$ power source of voltage $\epsilon_{0} \sin \omega_{t}$. The maximum current through the resistance is half of the maximum current through the power source. Then value of $R$ is
BITSATBITSAT 2016
Solution:
$\frac{i_{R_{0}}}{\sqrt{\left(i_{R_{0}}\right)^{2}+\left(i_{c_{0}}-i_{L_{0}}\right)^{2}}}=\frac{1}{2}$
$\Rightarrow \frac{\epsilon_{0} /R}{\sqrt{\left(\epsilon_{0} /R\right)^{2}\left(\epsilon_{0} \omega C-\frac{\epsilon_{0}}{\omega_{L}}\right)^{2}}}=\frac{1}{2}$
$\Rightarrow R=\frac{\sqrt{3}}{\left(\omega C-\frac{1}{\omega L}\right)}$