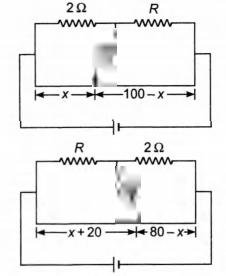
Q. A resistance of $2 \Omega$ is connected across one gap of a meter-bridge (the length of the wire is $100\, cm$) and an unknown resistance, greater than $2 \Omega$, is connected across the other gap. When these resistances are interchanged, the balance point shifts by $20\, cm$. Neglecting any corrections, the unknown resistance is
IIT JEEIIT JEE 2007Current Electricity
Solution:
$R > 2 \Omega \Rightarrow \, \, \therefore \, \, \, 100-x > x$
$Applying \, \, \, \, \, \, \, \, \, \frac{P}{Q} = \frac{R}{S}$
$We \, have \, \, \, \, \, \, \, \, \, \, \frac{2}{R} = \frac{x}{100 - x} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, ...(i)$
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \frac{R}{2} = \frac{x + 20}{80 - x} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, ...(ii)$
$Solving \, Eqs. \, (i) \, and \, (ii),\, we \, get, \, R = 3 \Omega$
$\therefore $Correct option is (a).