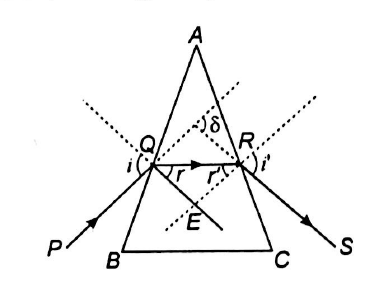
Question

A refracting angle of a prism is and the $ A $ Refractive index of the prism is $\cot \left( \frac{A}{2} \right) $ . Then, Angle of minimum deviation is:

• A. $ {{180}^{\circ }}-2A $
• B. $ {{90}^{\circ }}-A $
• C. $ {{180}^{\circ }}+2A $
• D. $ {{180}^{\circ }}-3A $

Answer 1

Answer: (A)

In the prism $A B C, \delta$ is the angle of minimum deviation, $A$ is angle of prism.

The refractive index of the material of the prism is given by
$\mu=\frac{\sin \left(\frac{A+\delta_{m}}{2}\right)}{\sin \frac{A}{2}}$
Given, $\mu=\cot \frac{A}{2}$,
$\cot \frac{A}{2}=\frac{\sin \left(\frac{A+\delta_{m}}{2}\right)}{\sin \frac{A}{2}}$
$\Rightarrow \frac{\cos \frac{A}{2}}{\sin \frac{A}{2}}=\frac{\sin \left(\frac{A+\delta_{m}}{2}\right)}{\sin \frac{A}{2}} $
$\Rightarrow \cos \frac{A}{2}=\sin \left(\frac{A+\delta_{m}}{2}\right)$
Using $\sin \left(\frac{\pi}{2}-\theta\right)=\cos \theta$, we have
$\Rightarrow \sin \left(\frac{\pi}{2}-\frac{A}{2}\right)=\sin \frac{A+\delta_{m}}{2} $
$\Rightarrow \delta_{m}=\pi-2 A=180^{\circ}-2 A$
Note : For a prism there is one and only one angle of minimum deviation.