Q.
A rectangular wire loop with length a and width b lies in the xy-plane as shown. Within the loop, there is a time dependent magnetic field given by $B = c [( x \cos \omega t ) \hat{ i }+( y \sin \omega t ) \hat{ k }]$
Here, $C$ and $\omega$ are constants. The magnitude of emf induced in the loop as a function of time is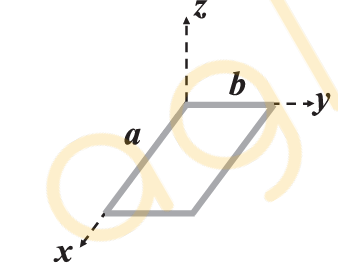
UPSEEUPSEE 2018
Solution: