Question

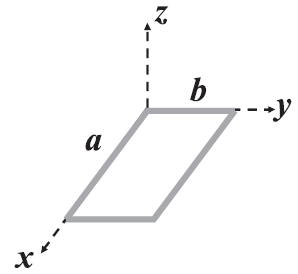
A rectangular wire loop with length $a$ and width $b$ lies in the $xy$ -plane as shown. Within the loop, there is a time dependent magnetic field given by $\overset{ \rightarrow }{B}= \, c\left[\left(x cos \omega t\right) \hat{i} + \left(y sin ⁡ \omega t\right) \hat{k}\right]$ .Here, $c$ and $\omega $ are constants. The magnitude of emf induced in the loop as a function of time is

• A. $\left|\frac{a b^{2} c}{2} \omega cos \omega t\right|$
• B. $\left|a b^{2} c \omega cos \omega t\right|$
• C. $\left|\frac{a^{2} b c}{2} \omega sin \omega t\right|$
• D. None of the options

Answer 1

Answer: (A)

from diagram only $z$ component of magnetic field gives flux.
Flux through small elemental area
$d\phi=ady \, cysin \left(\omega t\right)$
net flux $=acsin \omega t \displaystyle \int _{0}^{b} y \, d y$
$\phi=ac\frac{b^{2}}{2}sin \omega t$
$\therefore $ Induced emf in the loop.
$\epsilon =\frac{d}{d t}\phi_{m}=\frac{d}{d t}.\frac{a b^{2} c}{2}sin \omega t$
Hence, $\left|\epsilon \right|=\left|\frac{a b^{2} c}{2} \omega cos \omega t\right|$