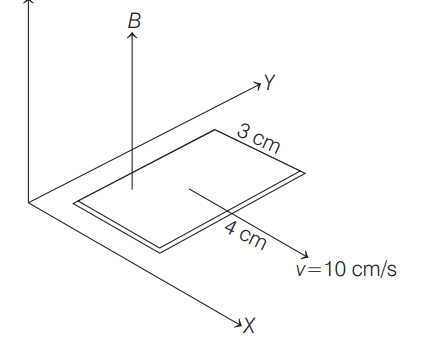
Question

A rectangular loop of wire is placed in the $XY$ - plane with its side of length $3\, cm$ parallel to the $X$ -axis and the side of length $4 \,cm$ parallel to the $Y$ - axis. It is moving in the positive $X$ - direction with the speed $10\, cm / s$. A magnetic field exists in the space with its direction parallel to the $Z$ - axis. The field decreases by $2 \times 10^{-3} \,T / cm$ along the positive $X$ - axis and increases in time by $2 \times 10^{-2} T / s$. The induced emf in the wire is

• A. $-4.8 \times 10^{-5} \,V$
• B. $4.8 \times 10^{-5}\, V$
• C. 0
• D. $3.6 \times 10^{-5} \,V$

Answer 1

Answer: (C)

Induced emf in wire = Rate of change of flux
$=\frac{d}{d t}(B A)=A\left\{\left(\frac{d}{d t} B\right)+v \frac{d}{d x} B\right\} $
$=12 \times 10^{-4}\left(2 \times 10^{-2}+10 \times 10^{-2} \times 2 \times 10^{-3}\right) $
$=12 \times 10^{-4}\left(2 \times 10^{-2}+2 \times 10^{-4}\right)$
$=24 \times 10^{-4}\left(10^{-2}+10^{-4}\right)=24 \times 10^{-5} \,V $
$=0.000024 \,V \simeq 0 \,V$