Question

A rectangular loop of sides $10\, cm$ and $5\, cm$ carrying a current $I$ of $12\, A$ is placed in different orientations as shown in the figure below.

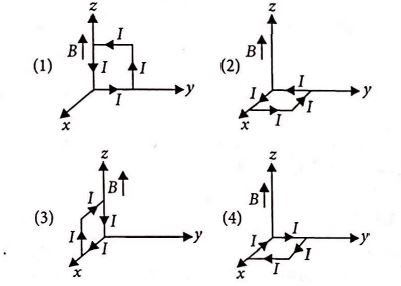
If there is a uniform magnetic field of $0.3\, T$ in the positive z-direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium.

• A. (2) and (4), respectively
• B. (2) and (3), respectively
• C. (1) and (2), respectively
• D. (1) and (3), respectively

Answer 1

Answer: (A)

$I = 12\,A$,
$\vec{B} = 0.3\,\hat{k} T$,
$A = 10 \times 5 \,cm^{2}$
$= 50 \times 10^{-4 }\,m^{2}$
$\overrightarrow{M} = IA \hat{n} = 12 \times50 \times 10^{-4}\hat{n}\,A\,m^{2}$
$= 6 \times 10^{-2}\, \hat{n}\, A \,m^{2}$
Here, $\overrightarrow{M_{1} } = 6 \times 10^{-2}\,\hat{i} \,A\,m^{2}$,
$\overrightarrow{M_{2} } = 6 \times 10^{-2}\,\hat{k} \,A\,m^{2}$
$\overrightarrow{M_{3} } = -6 \times 10^{-2}\,\hat{j} \,A\,m^{2}$,
$\overrightarrow{M_{4} } = -6 \times 10^{-2}\,\hat{k} \,A\,m^{2}$
$\overrightarrow{M_{2} }$ is parallel to $\vec{B}$, it means potential energy is minimum, therefore in orientation $\left(2\right)$ the loop is in stable equilibrium.
$\overrightarrow{M_{4} }$ is antiparallel to $\vec{B}$, it means potential energy is maximum, therefore in orientation $\left(4\right)$ the loop is in unstable equilibrium.