Question

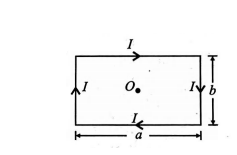
A rectangular loop of conductor of length $a$ and breadth $b$ carrying current $I$ is shown in the figure. The magnetic field at the centre $O$ of the loop is

• A. $\frac{\mu_{0} I(a+b)}{2 \pi \sqrt{a^{2}+b^{2}}}$
• B. $\frac{\mu_{0} I a b}{2 \pi \sqrt{a^{2}+b^{2}}}$
• C. $\frac{\mu_{0} I(a+b)}{\pi \sqrt{a^{2}+b^{2}}}$
• D. $\frac{2 \mu_{0} I \sqrt{a^{2}+b^{2}}}{\pi a b}$

Answer 1

Answer: (D)

The total magnetic field at $O$ due to current $I$ through rectangular loop is $B$.
Let $B_{1}, B_{2}, B_{3}$, and $B_{4}$ be the magnetic fields at $O$ due to current in arms $1,2,3$ and 4 respectively.
$\therefore B=B_{1}+B_{2}+B_{3}+B_{4}$
where $\left(B_{1}\right)=\left(B_{3}\right)$
$B_{1} =B_{3}=\frac{\mu_{0} I}{4 \pi(a / 2)}\left[\sin \left(90^{\circ}-\alpha\right)+\sin \left(90^{\circ}-\alpha\right)\right] $
$=\frac{\mu_{0} I}{4 \pi(a / 2)}(\cos \alpha+\cos \alpha)=\frac{\mu_{0} I \cos \alpha}{\pi a} $
$\left(B_{2}\right) =\left(B_{4}\right)=\frac{\mu_{0} I}{4 \pi(b / 2)}\left[\sin \left(90^{\circ}-\beta\right)+\sin \left(90^{\circ}-\beta\right)\right] $
$=\frac{\mu_{0} I}{4 \pi(b / 2)}(\cos \beta+\cos \beta)=\frac{\mu_{0} I \cos \beta}{\pi b}$
As $B_{1}, B_{2}, B_{3}$, and $B_{4}$ are acting in the same direction i.e. perpendicular to the plane of rectangular loop downwards.
$\therefore B=B_{1}+B_{2}+B_{3}+B_{4}$
or $ B=\frac{2 \mu_{0} I}{\pi}\left[\frac{\cos \alpha}{a}+\frac{\cos \beta}{b}\right]$
Putting $\cos \alpha=\frac{b}{\sqrt{a^{2}+b^{2}}} $ and $\cos \beta=\frac{a}{\sqrt{a^{2}+b^{2}}} $
we get, $ B=\frac{2 \mu_{0} I \sqrt{a^{2}+b^{2}}}{\pi a b}$