Q.
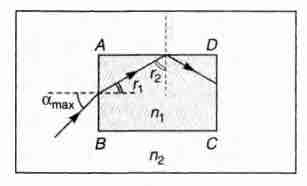
A rectangular glass slab ABCD of refractive index $n_1$ is A rectangular glass slab ABCD of refractive index $n_2(n_1 > n_2)$ A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence $\alpha_{max}$ such that the ray comes out only from the other surface CD, is given by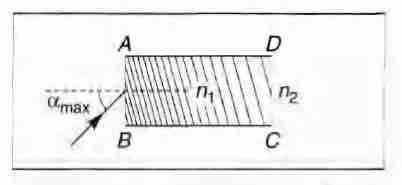
IIT JEEIIT JEE 2000
Solution:
Rays come out only from CD, means rays after refraction
from A B get total internally reflected at AD.
From the figure
$r_1+r_2=90^\circ$
$(r_1)_{max}=901^\circ-(r_2)_{min}and (r_2)_{min}=\theta_C$( for total internal reflection at AD)
where, $ sin\theta_C=\frac{n_2}{n_1}$
or $ \theta_C=sin^{-1}\Big(\frac{n_2}{n_1}\Big)$
$\therefore (r_1)_{max}=90^\circ-\theta_C$
Now, applying Snell's law at face A B
$\frac{n_1}{n_2}=\frac{sin\alpha_{max}}{sin(r_1)_{max}}$
$=\frac{sin \alpha_{max}}{sin(90^\circ-\theta_C}$
$=\frac{sin\alpha_{max}}{cos\theta_C}$
$or sin\alpha_{max}=frac{n_1}{n_2}cos \theta_C$
$\therefore \alpha_{max}=sin^{-1}\Bigg[\frac{n_1}{n_2}cos \theta_C\Bigg]$
$=sin^{-1}\Bigg[\frac{n_1}{n_2}cos sin^{-1}\Big(\frac{n_2}{n_1}\Big)\Bigg]$