Q.
A rectangular glass slab $A B C D$, of refractive index $n_{1}$, is immersed in water of refractive index $n_{2}\left(n_{1} > n_{2}\right) .$ A ray of light in incident at the surface $A B$ of the slab as shown. The maximum value of the angle of incidence $\alpha_{\max }$, such that the ray comes out only from the other surface $C D$ is given by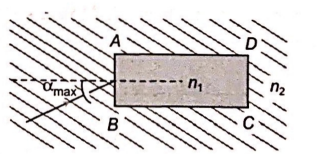
Ray Optics and Optical Instruments
Solution:
