Q.
A rectangular conducting loop of length $4 \sqrt{2} \, m$ and breadth 4 m carrying a current of 5 A in the anti-clockwise direction is placed in the xy-plane. The magnitude of the magnetic
induction field vector B at the intersection of the diagonals is
(Use $\mu_0 = 4 \pi \times 10^{-7} \, NA^{-2}$)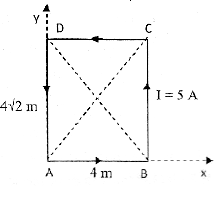
Solution: