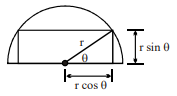
Q. A rectangle is inscribed in a given semicircle with one of its sides along the diameter. If $k$ times the area of the largest rectangle equals the area of the semicircle then the value of $k$ equals
Application of Derivatives
Solution:
Area of rectangle $=2 r \cos \theta \cdot r \sin \theta$
$=r^2 \sin 2 \theta \Rightarrow A_{\max .}=r^2 $
$\therefore k \cdot r^2=\frac{\pi r^2}{2} \Rightarrow k=\frac{\pi}{2}$