Q.
A ray parallel to principal axis is incident at $30^{\circ}$ from normal on concave mirror having radius of curvature $R$. The point on principal axis where rays are focussed is $Q$ such that $PQ$ is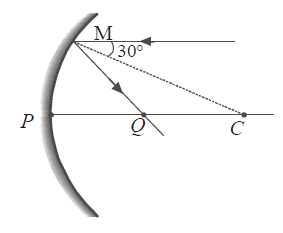
BITSATBITSAT 2015
Solution:
From similar triangles,
$\frac{Q C}{\sin 30^{\circ}}=\frac{R}{\sin 120^{\circ}}$
or $Q C=R \times \frac{\sin 30^{\circ}}{\sin 120^{\circ}}=\frac{R}{\sqrt{3}}$
Thus $P Q=P C-Q C=R-\frac{R}{\sqrt{3}}$
$=R\left(1-\frac{1}{\sqrt{3}}\right)$
