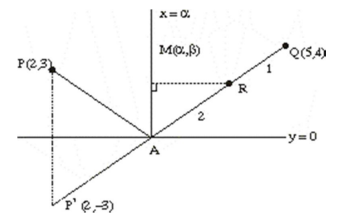
Q. A ray of light passing through the point $P(2,3)$ reflects on the $x$-axis at point $A$ and the reflected ray passes through the point $Q(5,4)$. Let $R$ be the point that divides the line segment $AQ$ internally into the ratio $2: 1$. Let the co-ordinates of the foot of the perpendicular $M$ from $R$ on the bisector of the angle PAQ be $(\alpha, \beta)$. Then, the value of $7 \alpha+3 \beta$ is equal to ______
Solution: