Q.
A ray of light passes through four transparent media with refractive indices $\mu_{1}, \mu_{2}, \mu_{3}$ and $\mu_{4}$ as shown in the figure. The surfaces of all media are parallel. If the emergent ray $C D$ is parallel to the incident ray $A B$, we must have :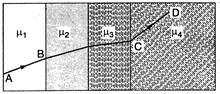
ManipalManipal 2004Ray Optics and Optical Instruments
Solution: