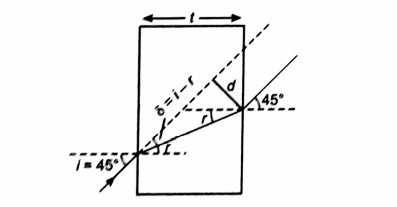
Question

A ray of light is incident on a surface of glass slab at an angle $45^{\circ} .$ If the lateral shift produced per unit thickness is $\frac{1}{\sqrt{3}} m$, the angle of refraction produced is

• A. $\tan ^{-1}\left(\frac{\sqrt{3}}{2}\right)$
• B. $\tan ^{-1}\left(1-\sqrt{\frac{2}{3}}\right)$
• C. $\sin ^{-1}\left(1-\sqrt{\frac{2}{3}}\right)$
• D. $\tan ^{-1}\left(\sqrt{\frac{2}{\sqrt{3}-1}}\right)$

Answer 1

Answer: (B)

Here, angle of incidence $i=45^{\circ}$

$\frac{\text { Lateral shift }( d )}{\text { Thickness of glass slab }( t )}=\frac{1}{\sqrt{3}}$
Lateral shift $d=\frac{t \sin \delta}{\cos r}=\frac{t \sin (i-r)}{\cos r}$
$\Rightarrow \frac{d}{t}=\frac{\sin (i-r)}{\cos r}$
or $\frac{d}{t}=\frac{\sin i \cos r-\cos i \sin r}{\cos r}$
or$\frac{d}{t}=\frac{\sin 45^{\circ} \cos r-\cos 45^{o} \sin r}{\cos r}$
$=\frac{\cos r-\sin r}{\sqrt{2} \cos r}$
or $\frac{d}{t}=\frac{1}{\sqrt{2}}(1-\tan r)$
or $\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{2}}(1-\tan r)$
or $\tan r=1-\frac{\sqrt{2}}{\sqrt{3}}$
or $r=\tan ^{-1}\left(1-\frac{\sqrt{2}}{\sqrt{3}}\right)$