Q.
A ray of light is incident on a prism as shown in the figure. The total deviation suffered by the ray is $\frac{x ^\circ }{2}$ . Then find $x$ . ( $\angle BAC=1^\circ $ and $\angle CAD=2^\circ $ , refractive indices are shown in figure.
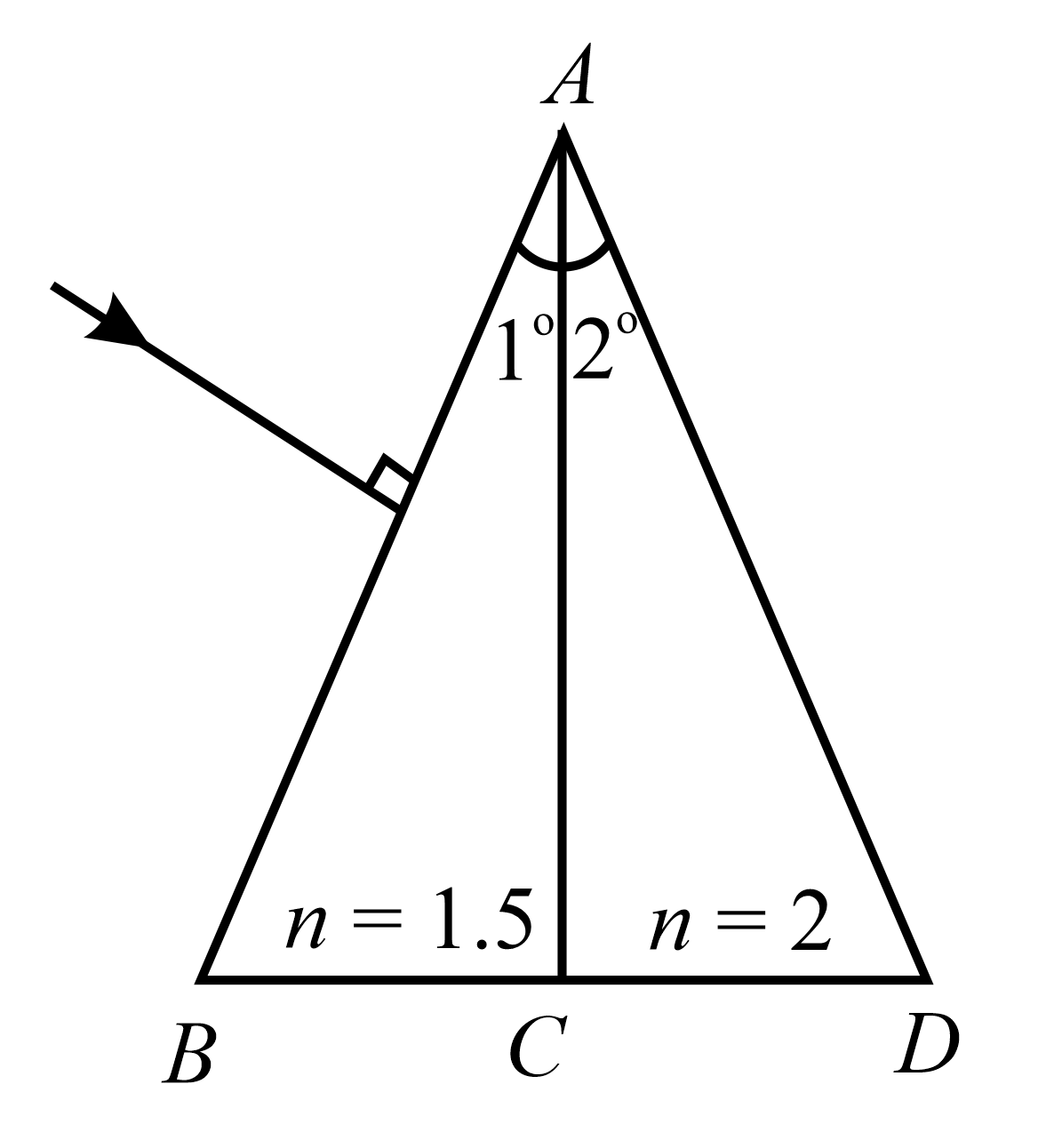
NTA AbhyasNTA Abhyas 2022
Solution: