Question

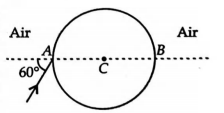
A ray of light falls on a transparent sphere with centre $C$ as shown in the figure. The ray emerges from sphere parallel to line $A B .$ The refractive index of sphere is

• A. $\mu=\sqrt{2}$
• B. $\mu=\sqrt{\frac{3}{2}}$
• C. $\mu=\sqrt{3}$
• D. $\mu=\sqrt{\frac{5}{2}}$

Answer 1

Answer: (C)

Apply Snell's law at points $A$ and $B$
$1 \sin 60^{\circ}=\mu \sin r \,\,\,\,\, \ldots( i )$
$\mu \sin r=1 \sin \phi\,\,\,\,\dots(ii)$
Solving equations (i) and (ii), we get $\phi=60^{\circ}$
Also, $2 r+180^{\circ}-\phi=180^{\circ}$
$2 r+180^{\circ}-60^{\circ}=180^{\circ}$
or $2 r=60^{\circ}$ or $r=30^{\circ}$
From equation (i), we get $\mu=\frac{\sin 60^{\circ}}{\sin ^{\circ}}=\frac{\sin 60^{\circ}}{\sin{cin} 30^{\circ}}=\sqrt{3}$