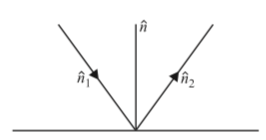
Q. A ray is incident on a plane surface. If $\hat{i} + \hat{j} - \hat{k}$ represents a vector along the direction of incident ray.$\hat{i} + \hat{j} $ is a vector along normal on incident point in the plane of incident and reflected ray, then vector along the direction of reflected ray is
Solution: