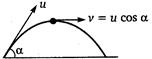
Q. A projectile is projected at an angle $60^{\circ}$ with horizontal with speed $10\, m/s$. The minimum radius of curvature of trajectory described by die projectile is
Delhi UMET/DPMTDelhi UMET/DPMT 2008Motion in a Plane
Solution:
The radius of curvature is given by
$\rho=\frac{m v^{3}}{|\vec{F} \times \vec{V}|}=\frac{m v^{3}}{F v \sin \theta}$
$=\frac{m v^{3}}{m g \sin \theta}$
$(\because F=m g)$
or $\rho=\frac{v^{2}}{g \sin \theta}$
$\therefore \rho_{\min }=\frac{v^{2}}{g(\sin \theta)_{\max }}$
$\therefore \rho_{\min }=v^{2} / g$
$(\because \theta_{\max }=90^{\circ}) \theta=90^{\circ}$
is only possible when the projectile is at the maximum height.
At the maximum height,
$v=u \cos \alpha=10 \cos 60^{\circ}=5 \,m / s$
$\therefore \rho_{\min }=\frac{5 \times 5}{9.8}=2.55\, m$