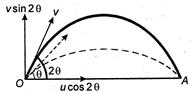
Q. A projectile is fired making an angle $ 2\theta $ with horizontal with velocity $4 \,m/s$. At any instant it makes an angle $ \theta , $ then its velocity is:
Jharkhand CECEJharkhand CECE 2006Motion in a Plane
Solution:
Horizontal component of velocity remains same.
Let $ v $ be the velocity, when projected with angle
$ \theta , $ then equating the horizontal velocities in both the cases, we get
$ v=\cos \theta =u\cos 2\theta $
$ \Rightarrow v=\frac{u\cos 2\theta }{\cos \theta } $
where $ \sec \theta =\frac{1}{\cos \theta } $
$ \therefore v=u\cos 2\theta \sec \theta $
Using $ \cos 2\theta =2{{\cos }^{2}}\theta -1, $
we get Given, $ u=4\,m/s,\, $
we get $ v=4(2\cos^{2}\theta -1)\sec\theta $
$ \Rightarrow v=4(2\cos\theta -\sec \theta ) $