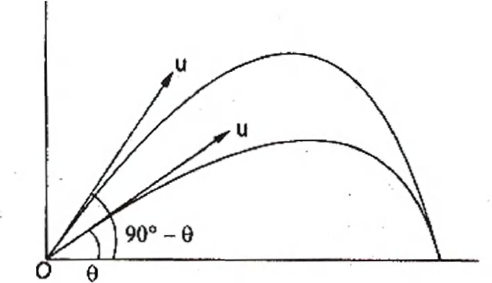
Q. A projectile can have the same range $R$ for two angles of projection. If $t_1$ and $t_2$ be the times of flights in the two cases, then the product of the two times of flights is proportional to :
AIEEEAIEEE 2005
Solution:
A .projectile can have same range if angles of projection are complementary i.e., 0 and $(90^° - \theta)$. Thus, in both cases :
$t_{1}=\frac{2u\,sin\,\theta}{g}\,...\left(i\right)$
$t_{2}=\frac{2u\,sin\,\left(90^{°}-\theta\right) }{g}$
$=\frac{2u\,cos\,\theta}{g}\,...\left(ii\right)$
From Eqs. $\left(i\right)$ and $\left(ii\right)$
$t_{1}t_{2}=\frac{4u^{2}\,sin\,\theta cos\,\theta }{g^{2}}$
$t_{1}t_{2}=\frac{2u^{2}\,sin\,2\theta }{g^{2}}$
$=\frac{2}{g} \frac{u^{2}\,sin\,2\theta}{g}$
$\therefore t_{1}t_{2}=\frac{2R}{g}\,\left(\therefore R=\frac{u^{2}\,sin\,2\theta}{g}\right)$
Hence, $t_{1}t_{2}\,\propto\,R$