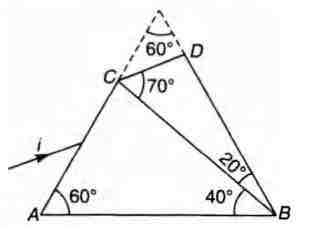
Question

A prism of refractive index $n_1$ and another prism of refractive index $n_2$ are stuck together with a gap as shown in the figure. The angles of the prism are as shown. $n_1 $ and $n_2$ depend on $\lambda$ the wavelength of light according to :
$n_1=1.20+\frac{10.8\times 10^4}{\lambda^2}and$
$ n_2=1.45+\frac{1.80\times10^4}{\lambda^2}$
where $\lambda$ is in nm.
(a) Calculate the wavelength $\lambda_0$ for which rays incident at any angle on the interface BC pass through without bending at that interface.
(b) For light of wavelength $\lambda_0$, find the angle of incidence i on the face AC such that the deviation produced by the combination of prisms is minimum.

Answer 1

$n_1=1.20+\frac{10.8\times 10^4}{\lambda^2_0}and n_2=1.45+\frac{1.80\times 10^4}{\lambda^2}$ Here, $\lambda$ is in nm (a) The incident ray will not deviate at B C if $n_1=n_2$,br> $\Rightarrow 1.20+\frac{10.8\times 10^4}{\lambda^2_0}and n_2=1.45+\frac{1.80\times 10^4}{\lambda^2_0}$ $\Rightarrow \frac{9\times 10^4}{\lambda^2_0}=0.25\, or\, \lambda_0=\frac{3\times 10^2}{0.5}$ $or \lambda_0=600nm$ (b) The given system is a part of an equilateral prism of prism angle $60^\circ$ as shown in figure. At minimum deviation. $ r_1=r_2=\frac{60^\circ}{2}=30^\circ=r $(say) $\therefore n_1=\frac{sin\, i}{sin\, r}$ $\therefore sin\, i\, =n_1.sin\, 30^\circ$ $sin\, i=\Bigg\{1.20+\frac{10.8\times 10^4}{(600)^2}\Bigg\}\Bigg(\frac{1}{2}\Bigg)=\frac{1.5}{2}=\frac{3}{4}$ $or $$ i=sin^{-1}$(3/4)