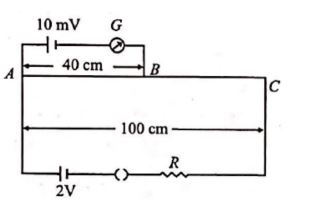
Question

A potentiometer wire of length $100 \,cm$ has a resistance of $10 \,\Omega$. It is connected in series with a resistance and a cell of emf $2 \,V$ and of negligible internal resistance. A source of emf $10 \,mV$ is balanced against a length of $40 \,cm$ of the potentiometer wire. What is the value of external resistance ?

• A. $790 \,\Omega$
• B. $890 \,\Omega$
• C. $990 \,\Omega$
• D. $1090 \,\Omega$

Answer 1

Answer: (A)

The current in the potentiometer wire $AC$ is $I=\frac{2}{10+R}$

The potential difference across the potentiometer wire is $V =$ current $\times$ resistance
$=\frac{2}{10+R} \times 10$
The length of the wire is $l = 100\, cm$.
So, the potential gradient along the wire is
$k=\frac{V}{l}=\left(\frac{2}{10+R}\right)\times\frac{10}{100}\quad\ldots\left(i\right)$
The source of emf $10\, mV$ is balanced against a length of $40 \,cm$ of the potentiometer wire
i.e. $10 \times 10^{-3}=k \times 40$
or $10 \times 10^{-3}=\frac{2}{\left(10+R\right)} \times \frac{40}{10}\quad$ (Using $(i)$)
or $R=790\,\Omega$.