Q.
A potential difference of 600 V is applied across the plates of a parallel plate condenser. The separation between the plates is 3 mm. An electron projected vertically, parallel to the plates, with a velocity of $2\times 10^6 m/s$ moves undeflected between the plates. Find the magnitude and direction of the magnetic field in the region between the condenser plates. (Neglect the edge effects). (Charge of the electron $= 1.6\times 10^{-19}C)$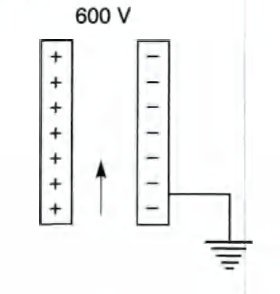
IIT JEEIIT JEE 1981Moving Charges and Magnetism
Solution:
Electron pass undeviated. Therefore,
$|F_e | = | F_m | or eE = eBv\, or\, B =\frac{E}{v}=\frac{V/d}{v}$
(V = potential difference between the plates)
$or B=\frac{V}{dv}$
Substituting the values, we have
$B=\frac{600}{3\times10^{-3}\times2\times10^6}=0.1 T$
Further, direction of $F_e$ should be opposite of $F_m$
$or eE\downarrow \uparrow e(v\times B$
$\therefore E\uparrow \downarrow v\times B$
Here, E is in positive x-direction
Therefore, $v\times B$ should be in negative x-direction or B
should be in negative z-direction or perpendicular to paper
inwards, because velocity of electron is in positive
y-direction.
