Q.
A positively charged sphere of radius $r_{0}$ carries a volume charge density $\rho$ (figure). A spherical cavity of radius $r_{0} / 2$ is then scooped out and left empty, as shown. $C_{1}$ is the centre of sphere and $C_{2}$ that of cavity. What is the direction and magnitude of the electric field at point $B$ ?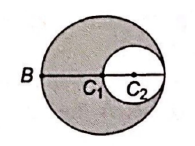
Electric Charges and Fields
Solution: