Q.
A positive point charge is released from rest at a distance $r _{0}$ from a positive line charge with uniform charge density.
The speed $(v)$ of the point charge, as a function of instantaneous distance ' $r$ ' from line charge, is proportional to $\sqrt{\ln \left(\frac{ r }{ r _{0}}\right)^{ N }}:$ The value of $\frac{1}{2 N }$ is ________.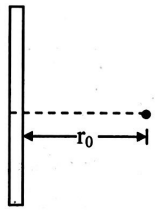
Electrostatic Potential and Capacitance
Solution:
