Question

A point source $S$ is placed at the bottom of different layers as shown in Fig. the refractive index of bottommost layer is $\mu_{0} .$ The refractive index of any other upper layer is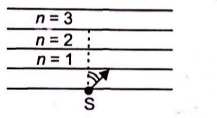

$\mu(n)=\mu_{0}-\frac{\mu_{0}}{4 \pi-18}$ where $n=1,2, \ldots$

A ray of light starts form the source $S$ as shown. Total internal reflection takes place at the upper surface of a layer having $n$ equal to

• A. 3
• B. 5
• C. 4
• D. 6

Answer 1

Answer: (C)

When $n=1$,
$\mu(1)=\mu_{0}-\frac{\mu_{0}}{4 \times 1-18}$
$ \Rightarrow \mu(1) > \mu_{0}$
When $n=2$,
$\mu(2)=\mu_{0}-\frac{\mu_{0}}{4 \times 2-18} $
$\Rightarrow \mu(2) > \mu_{0}$
When $n=4$
$\mu(4)=\mu_{0}-\frac{\mu_{0}}{4 \times 4-18}$
$\Rightarrow \mu(4) > \mu_{0}$
When $n=5$
$\mu(5)=\mu_{0}-\frac{\mu_{0}}{5 \times 4-18} $
$\Rightarrow \mu(5) < \mu_{0}$
Clearly, the total internal reflection shall take place at the top of a layer having $n=4$.