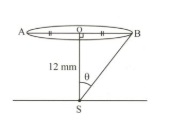
Question

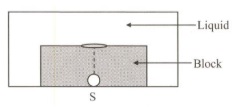
A point source $S$ is placed at the bottom of a $12 \, \text{mm}$ high transparent block of diamond(refractive index = $2.4$ ). The block is immersed in an optically rarer liquid as shown in the figure. It is found that the light emerging from the block to the liquid forms a circular bright spot of diameter $18 \, mm$ on the top of the block. What is the refractive index of the liquid?

Answer 1

As the light is passing from optically denser medium to rarer medium, let us assume $\theta $ is the critical angle.
From Pythagoras theorem,
$SB=\sqrt{SO^{2} + OB^{2}}=\sqrt{12^{2} + 9^{2}}=15mm$
$\therefore sin\theta =\frac{OB}{SB}=\frac{9}{15}=\frac{3}{5}$ $sin\theta =\frac{\mu _{2}}{\mu _{1}}=\frac{\mu }{2 . 4}$
$\therefore \frac{3}{5}=\frac{\mu }{2 . 4}$ $\Rightarrow \mu =1.44$