Q.
A point particle of mass $m$, moves along the uniformly rough track $PQR$ as shown in the figure. The coefficient of friction, between the particle and the rough track equals $\mu$. The particle is released, from rest, from the point $P$ and it comes to rest at a point $R$. The energies, lost by the ball, over the parts, $PQ$ and $QR$, of the track, are equal to each other, and no energy is lost when particle changes direction from $PQ$ to $QR$.
The values of the coefficient of friction $\mu$ and the distance $x(=QR)$, are, respectively close to :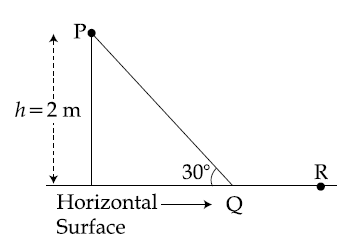
Solution: