Q.
A point $P$ moves in counter-clockwise direction on a circular path as shown in the figure. The movement of $'P'$ is such that it sweeps out a length $s = t^3 + 5$, where $s$ is in metres and $t$ is in seconds. The radius of the path is $20\, m$. The acceleration of $‘P’$ when $t\, =\, 2\, s$ is nearly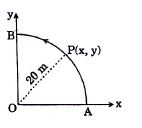
AIEEEAIEEE 2010Laws of Motion
Solution: