Question

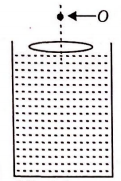
A point object $O$ is placed at a distance of $20 \,cm$ in front of a equiconvex lens $(^{a}\mu_{g} = 1.5)$ of focal length $10\, cm$. The lens is placed on a liquid of refractive index $2$ as shown in the figure. Image will be formed at a distance $h$ from lens. The value of $h$ is

• A. $5\,cm$
• B. $10\,cm$
• C. $20\,cm$
• D. $40\,cm$

Answer 1

Answer: (D)

As $ \frac{1}{f} =\left(\mu-1\right)\left[\frac{1}{R_{1}} -\frac{1}{R_{2}}\right] $
$ \frac{1}{10}= \left(1.5-1\right)\left(\frac{1}{R}+\frac{1}{R}\right) $
$ = 0.5 \times\frac{2}{R} $
$ \Rightarrow R = 10 \,cm $
$ \therefore \frac{\mu_{2}}{v}-\frac{\mu_{1}}{u} = \frac{\mu_{2}-\mu_{1}}{R}$
Refraction from first surface,
$\frac{1.5}{v_{1}} - \frac{1}{-20} = \frac{1.5-1}{+10} $
$ \Rightarrow v_{1} = \infty $
For the second surface,
$ \frac{2}{v} - \frac{1.5}{\infty} = \frac{2-1.5}{-10} $
$\Rightarrow v = -40\, cm $
$\therefore h = 40\, cm $