Question

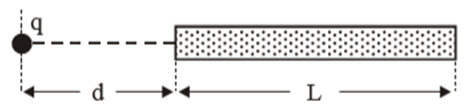
A point charge $q$ is situated at a distance $d$ from one end of a thin non-conducting rod of length $L$ having a charge $Q$ (uniformly distributed along its length) as shown in fig. Then the magnitude of the electric force between them is:

• A. $\frac{1}{4 \pi \varepsilon_0} \frac{q Q}{2 d(d+L)}$
• B. $\frac{1}{\pi \varepsilon_0} \frac{2 q Q}{d(d+L)}$
• C. $\frac{1}{4 \pi \varepsilon_0} \frac{q Q}{3 d(d+L)}$
• D. $\frac{1}{4 \pi \varepsilon_0} \frac{q Q}{d(d+L)}$

Answer 1

Answer: (D)

$F=\displaystyle \int _{d}^{d + L}\frac{k q d q}{x^{2}}=\displaystyle \int _{d}^{d + L}\frac{k q \left(\frac{Q}{L} d x\right)}{x^{2}}=\frac{k q Q}{L}\displaystyle \int _{d}^{d + L}\frac{1}{x^{2}}dx$
$F=\frac{k q Q}{d \left(\right. d + L \left.\right)}=\frac{1}{4 \pi \left(\epsilon \right)_{0}}\frac{q Q}{d \left(\right. d + L \left.\right)}$
Or

The linear charge density of rod $\lambda =\frac{Q}{L};$
$dq=\lambda dx$
Force due to small element $dx$ to charge $q$
$dF=\frac{1 \left(\right. q \left.\right) \left(\right. \lambda \left.\right) d x}{4 \pi ϵ_{0} x^{2}}$
Total force in-between point charge and rod
$F_{n e t}=\frac{q Q}{L}\displaystyle \int _{d}^{L + d}\frac{x^{- 2} d x}{4 \pi ϵ_{0}}=\frac{q Q}{4 \pi ϵ_{0} L}\left[- \frac{1}{x}\right]_{d}^{L + d}$
$=\frac{q Q}{4 \pi \epsilon _{0} L}\left[\frac{1}{d} - \frac{1}{L + d}\right]$
$=\frac{q Q}{4 \pi ϵ_{0}}\left[\frac{1}{\left(\right. d \left.\right) \left(\right. L + d \left.\right) \left.\right)}\right]$