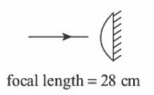
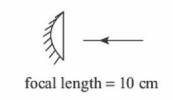
Q.
A planoconvex lens becomes an optical system of $28\, cm$ focal length when its plane surface is silvered and illuminated from left to right as shown in Fig-A.
If the same lens is instead silvered on the curved surface and illuminated from other side as in Fig.B, it acts like an optical system of focal length $10 \,cm$ . The refractive index of the material of lens is :
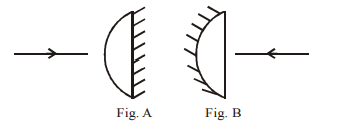
Solution: