Q.
A plano-convex lens $\left(\mu \, = \frac{3}{2}\right)$ has a radius of curvature $R=15 \, cm$ and is placed at a distance $z$ from a concave lens of focal length $20 \, cm$ as shown. At what distance $x_{0}$ should a point object be placed from the plano-convex lens, so that position of the final image is independent of $z$ ?
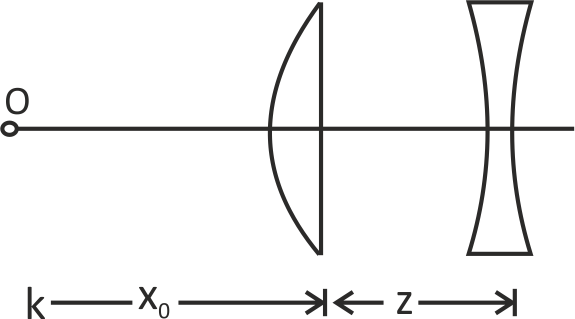
NTA AbhyasNTA Abhyas 2020Ray Optics and Optical Instruments
Solution: