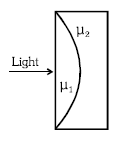
Q. A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive indices $\mu_1$ and $\mu_2$ and $R$ is the radius of curvature of the curved surface of the lenses, then the focal length of combination is
Solution:
Equivalent focal length is given by $\frac{1}{f_{eq}} = \frac{1}{f_{1}} + \frac{1}{f_{2}}$
$ \frac{1}{f_{eq}} = \left(\mu_{1}- 1\right)\left(\frac{1}{\infty} - \frac{1}{-R}\right)+ \left(\mu_{2} -1\right)\left(\frac{1}{-R} - \frac{1}{\infty}\right)$
$ \Rightarrow f_{eq} = \frac{R}{\mu_{1} - \mu_{2}}$