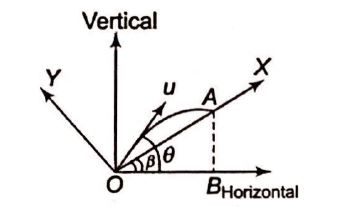
Question

A plane surface is inclined making an angle $\beta$ above the horizon. A bullet is fired with the point of projection at the bottom of the inclined plane with a velocity $u$ ; then the maximum range is given by:

• A. $\frac{u^{2}}{g}$
• B. $\frac{u^{2}}{g\left(1+sin \,\beta \right)}$
• C. $\frac{u^{2}}{g\left(1-sin\, \beta \right)}$
• D. $\frac{u^{2}}{g\left(1+cos \,\beta \right)}$

Answer 1

Answer: (B)

Suppose the particle be projected with a velocity $u$ making an angle $\theta$ with the horizontal. Suppose the particle strikes the inclined plane at A after time $T$. If $x$-axis is taken along the inclined plane and y-axis normal to the inclined plane. Then

$u_{x} =u$ cos $(\theta - \beta )$,
$ u_{y} = u$ sin$(\theta - \beta )$
During the time of flight $T$, the displacement along y-axis is zero.
Using equation
$s_{y} =u_{y}t+\frac{1}{2} a_{y}t^{2}$
$0=u$ sin $(\theta -\beta)T+\frac{1}{2} (-g \,cos \,\beta)T^{2}$
$T=\frac{2 \,u \,sin (\theta -\beta)}{g\,\,cos\,\,\beta}$
Component of velocity along horizontal $= u$ cos $\theta$.
Distance covered along horizontal
$OB =(u\,cos \,\beta)T$
$=u\,cos\, \theta[\frac{2u\,sin(\theta-\beta)}{g\,cos\,\beta}]$
$=\frac{2u^{2}\,cos\, \theta \,sin(\theta-\beta)}{g\,cos\, \beta}$
Range $R = OA$
$OA =\frac{OB}{cos\,\beta} $
$=\frac{2u^{2} \,cos\, \theta \,\sin(\theta-\beta)}{g\, cos^{2} \theta}$
$R=\frac{2u^{2} \,cos \, \theta\,sin (\theta-\beta)}{g\, cos^{2}\,\beta}$
$=[\frac{u^{2}}{g\,cos^{2} \, \beta}][2\, sin(\theta - \beta) cos\, \theta]$
$= \frac{u^2}{g\,cos^2\,\beta} [\sin(2\theta - \beta) - \sin\,\beta]$
For a given u and $\beta, R$ is maximum, when sin $(2 \theta - \beta)$ is maximum, i.e., when
sin $(2\theta-\beta) =1\, or\, 2\theta -\beta =\frac{\pi}{2}$
or $2\theta=\beta+\frac{\pi}{2}$ or $\theta=\frac{\beta}{2}+\frac{\pi}{2}$
Hence, the angle of projection $\theta$, for maximum range up the inclined plane is given by
$\theta =\frac {\beta}{2} +\frac{\pi}{4}$
$R_{max} =\frac{u^{2}}{g\, cos^{2}\, \beta} [1-sin \, \beta]$
$= \frac{u^{2}(1-sin\, \beta)}{g(1-sin^{2}\, \beta)} $
$=\frac{u^{2}}{g(1+sin\, \beta)}$