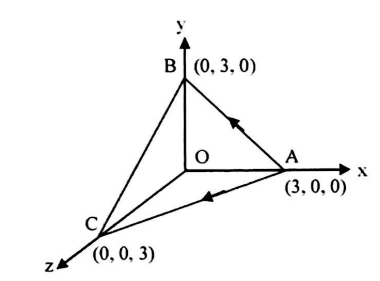
Question

A plane is parallel to two lines whose direction ratios are $(1,0,-1)$ and $(-1,1,0)$ and it passes through the point $(1,1,1)$, cuts the axis at $A, B, C$, then find the volume of the tetrahedron $O A B C$.

Answer 1

Let equation of plane
$a(x-1)+b(y-1)+c(z-1)=0$
and $a-c=0$ ...(1)
$-a+ b=0$
$a=b=c=\lambda,$ from $(1)$
$\lambda(x-1)+\lambda(y-1)+\lambda(z-1)=0$
$x+y+z=3$

Volume $=\frac{1}{6}[\overrightarrow{ OA }\,\, \overrightarrow{ OB }\,\, \overrightarrow{ OC }]$
$=\frac{1}{6}\begin{vmatrix}3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3\end{vmatrix}$
$=\frac{3 \times 3 \times 3}{6}=\frac{9}{2}$