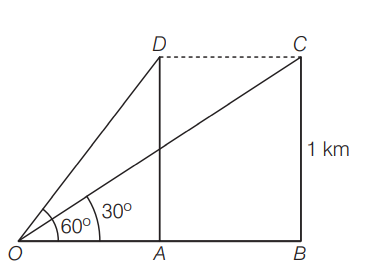
Question

A plane is flying horizontally at a height of $1\,Km$ from ground. Angle of elevation of the plane at a certain instant is $60^{\circ}$. After $20$ seconds angle of elevation is found $30^{\circ}$. The speed of plane is

• A. $\frac{100}{\sqrt{3}}m /s$
• B. $\frac{2 00}{\sqrt{3}}m /s$
• C. $100 \sqrt{3}m /s$
• D. $200 \sqrt{3}m /s$

Answer 1

Answer: (A)

Let $A D$ be the height at which the plane is flying i.e.
$1\, km =1000\, m$ and $C$ be the position of the plane after $20\, s$.
It is given that, $\angle A O D=60^{\circ}$ and $\angle B O C=30^{\circ}$

In right angled $\Delta O A D$ and $\Delta O B C$, we have
$\tan 60^{\circ}=\frac{A D}{O A}$ and $\tan 30^{\circ}=\frac{B C}{O B}$
$\Rightarrow O A=\frac{1000}{\sqrt{3}}$ and $\frac{1}{\sqrt{3}}=\frac{1000}{O B}$
$[\because 1 km =1000\, m ]$
$\Rightarrow O A=\frac{1000}{\sqrt{3}} m$ and $O B=1000 \sqrt{3} m$
$[\because A D=B C=1000\, m ]$
$\Rightarrow $ Now, $O A+A B=1000 \sqrt{3}$
$\Rightarrow A B=1000 \sqrt{3}-\frac{1000}{\sqrt{3}}$
$\Rightarrow A B=\frac{3000-1000}{\sqrt{3}}=\frac{2000}{\sqrt{3}} m$
$\therefore $ Speed $=\frac{\text { Distance }}{\operatorname{Time}}=\frac{2000}{\sqrt{3} \times 20}=\frac{100}{\sqrt{3}} m / s$