Q.
A perfectly reflecting mirror of mass M mounted on a spring constitutes a spring-mass system of angular frequency $\Omega$ such that $\frac{4\pi M\Omega}{h} = 10^{24} m^{-2}$ with h as Planck’s constant. N photons of wavelength $\lambda = 8\pi \times 10^{-6}$ m strike the mirror simultaneously at normal incidence such that the mirror gets displaced by 1 \mu m. If the value of N is $x \times 10^{12}$, then the value of x is _____.
[Consider the spring as massless]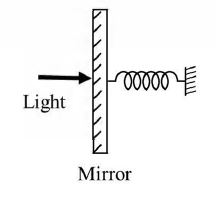
JEE AdvancedJEE Advanced 2019
Solution: