Question

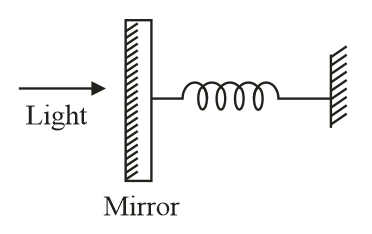
A perfectly reflecting mirror of mass $M$ mounted on a spring constitutes a spring-mass system of angular frequency $\Omega$ such that $\frac{4 \pi M \Omega}{h}=10^{24}m^{- 2}$ with $h$ as Planck's constant. $N$ photons of wave- length $\lambda =8\pi \times 10^{- 6}m$ strike the mirror simultaneously at normal incidence such that the mirror gets displaced by $1\mu m.$ If the value of $N$ is $x\times 10^{12},$ then the value of $x$ is

Answer 1

Total Momentum transferred on mirror $=\frac{2 N h}{\lambda }$ (for perfect reflection)
In an $SHM$
$V_{m a x}=A.\Omega$
Where $A=$ amplitude and $\Omega=$ angular frequency
$V_{(\text {mean position })}=\Omega A$ (where $\left.A=1 \mu m\right)$
$\Rightarrow \frac{2 N h}{\lambda}=M \Omega A\left(\right.$ where $\left.\lambda=8 \pi \times 10^{-6}\right)$
$\therefore N=\frac{\lambda M \Omega A}{2 h}$
$\Rightarrow N=\frac{M \Omega 10^{- 6} \lambda }{2 h}=\frac{M \Omega 8 \pi \times 10^{- 6} \times 10^{- 6}}{2 h}$
$N=\frac{4 \pi M \Omega}{h}\times 10^{- 12}$
$=10^{24}\times 10^{- 12}$
$N=1\times 10^{12}$
$x=1$